공통수학 상 1단원 다항식.
① 다항식 연산
② 항등식
③ 나머지 정리
④ 인수분해
다항식 단원은 고등수학의 가장 기초가 되는 식의 연산을 다루고 있다. 식을 어떻게 전개하고 분해하고 어떻게 표현할 것인지 공부하는 단원이다. 그 중 다항식의 연산 단원은 출제되는 문제들이 난이도가 대부분 쉽기 때문에 학생들이 쉽게 쉽게 넘어가지만 고난도 문제의 풀이과정에서 식을 다루는 방법에 따라 연산의 효율 면에서 큰 차이가 생긴다. 사소한 것 같지만 정해진 시간 내에 문제를 푸는 시험에서는 성적을 가르는 중요한 요소가 된다.
① 다항식 연산
우리는 다항식의 곱셈을 분배법칙을 통해 전개하라고 배운다. $(a+b)^2 $ 을 분배법칙을 써서 전개하면 다음과 같다. $$ (a+b)^2=(a+b)(a+b)=a^2+2ab+b^2 $$
위 식을 전개하는 거는 누구나 다 한다. 저 식의 의미를 생각해보자. 식 $(a+b)$ 를 제곱하면 $ a^2,2ab,b^2 $ 의 합과 같다는 것이다. 여기서 중요한 점은 식의 곱셈이 항들의 합으로 표현되었다는 것이다. 무슨 말이냐면, $a=1,b=2$ 일 때 $(a+b)^2=3^2=9$ 이다. 그런데 이 9라는 수는 위의 전개식에 의해 $9=1^2+2\cdot 1\cdot 2+2^2=1+4+4$ 로 똑같이 연산이 된다. 그래서 다항식의 곱셈을 전개한다는 것의 의미는, 곱셈(9)을 항들의 합(1+4+4)으로 보겠다는 것이다. 결국 곱셈의 전개식에서는 덧셈으로 이루어진 항들이 중요해진다.

곱셈공식에서도 우리가 잘 봐야 할 것은 덧셈으로 이어진 항이다. 수 많은 전개식들 중 특별한 몇 가지를 곱셈공식이라고 이름을 붙여 외우는 것은 앞으로 많이 나오게 될 식들을 외워서 자유롭게 쓰겠다는 말이다. 그럼 잘 써먹기 위해서, 우리가 집중해야 할 포인트는 공식을 이루는 항들이 어떤 것이냐 는 데에 있다. $(x+y)^3$ 은 $x^3,3x^2 y,3xy^2,y^3$의 항들로 이루어져 있고 반대로 이 4개의 항으로 $(x+y)^3$을 구성할 수 있다. 곱셈공식을 이해한다는 것은 식을 이루는 항들을 잘 안다는 것이고 그래서 가장 대표적인 곱셈공식 문제는 공식을 이루는 항들의 값을 물어보는 식으로 출제된다.

교과서에 나와 있는 곱셈공식 예제다. $x+y,xy$의 값을 알 때 $x^3+y^3$의 값을 구하라.
곱셈공식 2번에 항에 $x^3,y^3$ 이 있으니까 공식 2번을 이용하자.$$ (x+y)^3=x^3+3x^2 y+3xy^2+y^3=27 $$
저 4개의 항들 중에 $x^3+y^3$ 이 있으니까 $3x^2 y+3xy^2$ 의 값만 알면 구할 수 있을 것 같다. 문제에서 주어진 조건 $xy=1$ 을 이용하기 위해 봤더니 $3x^2 y+3xy^2=3xy(x+y)$ 이고 $x+y,xy$ 값을 모두 알고 있으니 답을 구할 수 있다. $$ x^3+y^3=27-(3x^2 y+3xy^2)=27-3xy(x+y)=27-3\cdot 1\cdot 3=18 $$
이 예제는 결국 $x^3,y^3$ 이 구성하는 곱셈공식이 무엇인지를 물어보고 있다. 그래서 학생들은 어떤 항을 보았을 때 적절한 곱셈공식을 떠올릴 수 있는 방향으로 공부가 되어야 한다. 단순히 전개결과를 외우는 것은 공부가 되지 않는다.
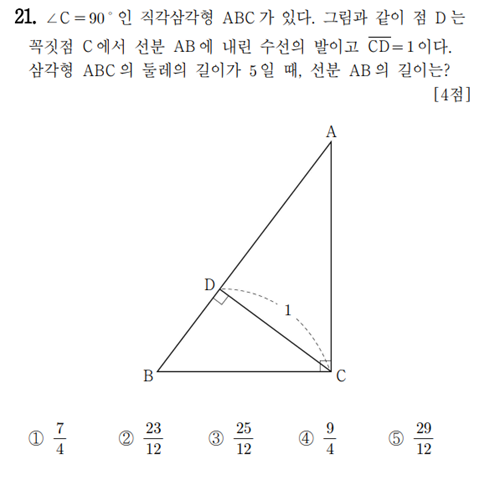
정답률 30%짜리 고1 문제를 풀어보자.
큼지막한 조건을 먼저 체크해보면
①직각삼각형ABC
② $\overline{CD}=1$
③삼각형ABC 둘레 길이=5
③조건을 이용하기 위해 세 변의 길이를 문자로 나타낼 필요가 있다.
$\overline{BC}=x,\overline{AC}=y,\overline{AB}=z $라고 하고 각 조건을 이용하면
① 피타고라스 정리 $x^2+y^2=z^2$
② 삼각형 넓이 $xy=z$
③ $x+y+z=5$
이때 $z$ 의 값을 구하라는 문제이다. 세 식을 잘 풀어서 $z$를 구해야 하는데 이게 관건이다. $x$에 관해서 정리를 해야 할지 $y$ 에 관해서 정리를 해봐야 할지 식을 어떻게 연립해야 할지 혼란스럽다. 그러나 수학 1등급 명품이는 ① 의 $x^2,y^2$ 와 ②의 $xy$ 를 보고 중학교 곱셈공식을 떠올린다. $$(x+y)^2=x^2+2xy+y^2$$
을 이용하면
$$(x+y)^2=x^2+2xy+y^2=z^2+2z$$
③에서 $x+y=5-z$ 이므로
$$(x+y)^2=(5-z)^2=z^2+2z$$ $$z^2-10z+25=z^2+2z$$ $$25=12z$$ $$z=\frac{25}{12}$$
곱셈공식을 아무 생각 없이 외우기만 하면 이런 문제를 풀기 힘들다. $(x+y)^2$을 외워서 전개는 누구나 다 하지만 항으로 $(x+y)^2$ 을 만들어 낼 수 있는 것은 상위권 학생들 뿐이다. 시험에서는 이런 기초적인 부분에서 풀이의 속도가 결정이 되고 결국 성적이 결정된다. 언제든지 이용할 수 있게 우리는 공식에 있는 항들에 집중을 해야 하고 평소에 연습이 되어 있어야 한다. 곱셈공식의 의미는 단순한 전개식이라는 것 보다 항들의 합으로 표현될 수 있다는 데에 있다.
'수학 > 고1' 카테고리의 다른 글
| Ⅵ. 경우의 수. 순열 (1) | 2024.11.03 |
|---|---|
| Ⅵ. 경우의 수. 합과 곱의 법칙 (3) | 2024.10.29 |
| Ⅱ. 방정식과 부등식. 이차방정식과 이차함수의 관계(2) (2) | 2024.10.23 |
| Ⅱ. 방정식과 부등식. 이차방정식과 이차함수의 관계(1) (3) | 2024.10.21 |
| Ⅱ. 방정식과 부등식. 근과 계수의 관계 (1) | 2024.10.15 |




댓글